Oui, il existe des moyens de le mesurer, bien qu'il existe de nombreux algorithmes différents prétendant être plus corrects que les autres. Cette formule de Vassilakis est récente (2007).

Elles mesurent la " rugosité", qui est similaire à la dissonance. (La dissonance est essentiellement la rugosité, mais pondérée vers certains intervalles en raison du conditionnement culturel, ce qui est évidemment difficile à mesurer quantitativement.) Pour deux tons sinusoïdaux, la rugosité par rapport à la différence de fréquence ressemble à ceci:

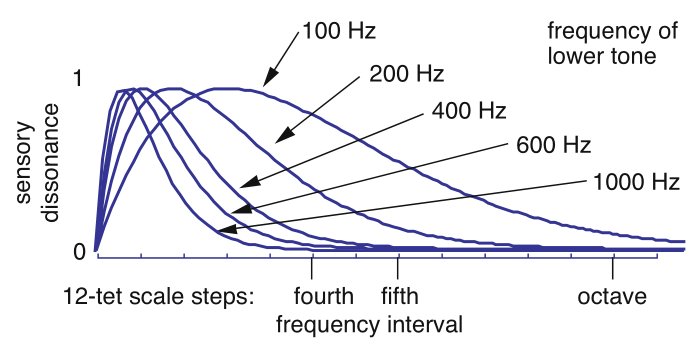
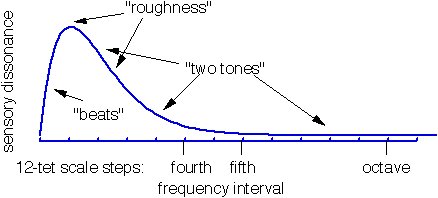
(Source: William A. Sethares)

Pour les signaux plus complexes, composés de plusieurs tonalités:

La rugosité des signaux correspondant à des spectres avec plus de deux composantes sinusoïdales est calculée en additionnant la rugosité de toutes les paires sinusoïdales du spectre.

Pour les tons avec des spectres harmoniques, l'effet net de la rugosité entre toutes les harmoniques présentes produit des graphiques avec des encoches de consonance à des intervalles que nous connaissons bien, comme 3: 2 quinte parfaite:

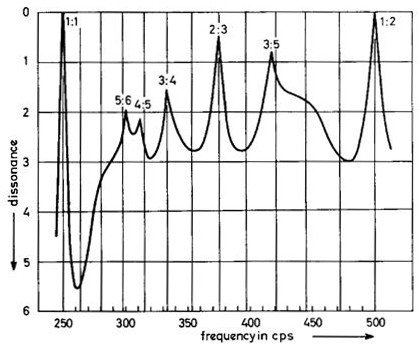
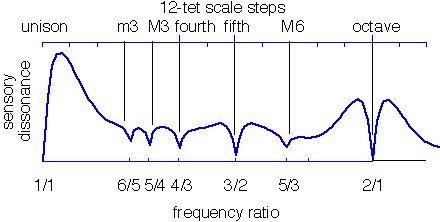
La courbe noire provient de l'ancien article Plomp-Levelt 1965, avec cette description:

Nous supposons que la dissonance totale d'un tel intervalle est égal à la somme des dissonances de chacun paire de partiels adjacents ... ces présuppositions sont plutôt spéculatives ... De cette façon, les courbes ... ont été calculées pour des tons complexes composés de 6 harmoniques. ... montre comment la consonance de certains intervalles, donnée par de simples rapports de fréquence, dépend de la fréquence.

(Ainsi, la courbe Plomp-Levelt est basée sur la somme de la rugosité des partiels adjacents tandis que Vassilakis additionne " toutes les paires sinusoïdales". (Sethares m'a écrit et dit que la chose "adjacente" est simplement parce que la puissance de calcul était limitée dans les années 60. Comparer chaque paire est plus approprié.))

De plus amples descriptions de cette courbe peuvent être trouvées dans Marc Leman - Fondements de la musicologie comme science du traitement de contenu (qui parle également de dériver le slendro et le pelog échelles du même algorithme appliqué aux instruments de gong inharmoniques) et Rapport caché de Plomp et Levelt

La courbe bleue provient de Sethares Relating Tuning and Timbre, qui utilise ce calcul MATLAB, également basé sur les courbes Plomp-Levelt. (Et voici ma traduction Python.) Voici une application basée sur MATLAB qui utilise le modèle Vassilakis 2007 pour calculer également la même courbe pour 6 harmoniques (et a le M3 comme plus consonne que le m3).

Vous pouvez voir que les deux courbes ne sont pas d'accord sur la question de savoir si le m3 ou M3 est plus consonne. Je ne sais pas si cela est dû au calcul uniquement des partiels adjacents par rapport à tous les partiels ou si les partiels ont des amplitudes différentes ou quoi. Bien sûr, les vrais instruments produisent beaucoup de variations dans leurs spectres harmoniques, même en jouant la même note sur le même instrument, donc ces courbes sont toutes des approximations intrinsèques. Voici un tracé que j'ai fait du violon contre la clarinette, montrant que le M3 est plus consonne lorsque le violon joue la note la plus élevée, car les clarinettes produisent principalement des harmoniques impaires.

Aussi, pour plus de 2 tons, l'algorithme Sethares classe les accords mineurs et majeurs comme également consonnants, ce qui n'est pas l'interprétation habituelle. Ainsi, Erlich et Monzo interprètent le nombre de Sethares comme une simple mesure de la "rugosité" et exigent que la "dissonance" inclue à la fois la "rugosité" et la "tonalité", où les accords majeurs sont plus consonnants parce qu'ils sont plus proches de la racine d'une série harmonique (4: 5: 6) tandis que les accords mineurs sont plus éloignés (10:12:15). Je ne connais cependant pas de moyen de quantifier cela pour des fréquences arbitraires.

Oui. Cela a à voir avec le rapport de leurs fréquences. Essentiellement, plus les nombres impliqués sont petits, mieux c'est.

L'unisson parfait, avec un rapport 1: 1 (par exemple, C joué avec le même C), a une consonance parfaite. C au G suivant a un rapport 2: 3; la quinte parfaite est la deuxième plus consonne. La seconde mineure (par exemple, Do à Do #) est la plus dissonante dans les échelles occidentales avec un rapport de fréquence de 15:16.

Cela représente la fréquence à laquelle les ondes sonores "correspondent". Chaque troisième cycle d'un C correspond à chaque deuxième cycle d'un G, et vice versa; c'est-à-dire que les pics des ondes se produisent en même temps tous les deux cycles (ou trois cycles, selon la note que vous choisissez comme base). C'est souvent! Donc dans l'ensemble, votre oreille perçoit les sons comme étant synchronisés et mélodieux. En revanche, les ondes qui correspondent rarement, comme la seconde mineure avec seulement la correspondance du 15e (16e) cycle, sont largement désynchronisées et donc dissonantes.

L'esprit est étrange et ce que l'on perçoit la dissonance n'est pas nécessairement ce qu'un autre percevrait comme une dissonance. Cela dit, le plus proche que vous obtiendrez d'une mesure objective absolue est le logarithme de base 2 du multiple le moins commun des côtés du rapport. Par exemple:

 lg (LCM (15, 16)) = lg (240) ~ = 7.9 

C'est environ 3 fois plus que

 lg (LCM (2, 3)) = lg (6) ~ = 2.6 

Soigneusement,

 lg (LCM (1, 1)) = lg (1) = 0 

donc cela reflète également le fait que l'unisson parfait n'a pas de dissonance. Fait intéressant, Euler semblait penser que le LCM était également le moyen de le faire ¹ .

(Notez que LCM (x, y) = x * y pour des rapports entièrement réduits; par exemple, 2: 3 plutôt que 4: 6.)

[1]: Knobloch, Eberhard (2008). Euler Transgressing Limits: The Infinite and Music Theory. Quaderns d’Història de l’Enginyeria, IX , 9-24. Disponible en ligne: http://upcommons.upc.edu/revistes/bitstream/2099/8052/1/article2.pdf

L'utilisation de la formule empirique A + B divisée par AB où A et B représentent le rapport de fréquence des deux notes de cet intervalle semble donner une mesure absolue de la grandeur du degré de consonance comme suit

Le rapport de fréquence à l'unisson 1: 1 donne une valeur de 2

Le rapport de fréquence d'octave 2: 1 donne une valeur de 1,5

Le rapport de 5e fréquence parfait 3: 2 donne une valeur de 0,833

Le rapport 4: 3 parfait de 4e fréquence donne une valeur de 0,583

Le rapport de 6e fréquence majeur 5: 3 donne une valeur de 0,533

Majeur Le rapport de 3e fréquence 5: 4 donne une valeur de 0,45

Le rapport de 3e fréquence mineur 5: 6 donne une valeur de 0,366

Le rapport de 6e fréquence mineur 5: 8 donne une valeur de 0,325

Rapport de deuxième fréquence majeur 8: 9 donne une valeur de 0,236

Rapport de fréquence 7e majeur 8:15 donne une valeur de 0,192

Mineur 7e rapport de fréquence 9:16 donne une valeur de 0,174

Le rapport de 2e fréquence mineur 15:16 donne une valeur de 0,129

Bien que la formule utilisée soit empirique, les résultats sont conformes notablement proche de l'ordre accepté du degré de consonance des intervalles harmoniques dans une octave

Il y a une réponse courte et une réponse plus longue et plus compliquée; Je vais juste donner la réponse courte ici avec les bases les plus simples de la réponse longue.

La réponse courte est: Oui, il y en a, en quelque sorte. Si vous prenez le rapport des fréquences des deux hauteurs, vous obtiendrez une fraction dans les termes les plus bas. Plus les nombres de cette fraction sont petits, plus l'intervalle est consonne. Par exemple, deux hauteurs à l'unisson ont un rapport 1: 1. Une octave a un rapport de 2: 1. Une quinte parfaite (telle que C à G) a un rapport de 3: 2, etc. Matthew fait du bon travail dans sa réponse, expliquant pourquoi les rapports avec des nombres plus petits semblent plus consonnants que les rapports avec des nombres plus grands. / p>

Mais tout cela est rendu plus compliqué par le tempérament, qui est la façon dont les hauteurs sont accordées les unes par rapport aux autres. Voyez, supposons que vous accordiez votre A à 440 Hz, puis que vous commenciez à accorder les autres notes par rapport à ce A, en utilisant les ratios de nombres entiers comme guide. Vous accorderez E à 660 Hz, par exemple. Pour les premières notes, tout sonnera bien, mais il ne faudra pas longtemps avant que vous commenciez à entendre des intervalles étranges. Certains intervalles ont de bons rapports de nombres entiers, mais d'autres qui, selon vous, devraient sonner bien, comme la tierce majeure de Eb à G, sonnent vraiment mal. Pour faire court, il s’avère impossible d’accorder les douze notes chromatiques en utilisant des rapports de fréquences entiers et de faire en sorte que tout se passe bien. Mathématiquement, cela ne peut tout simplement pas être fait.

Vous devez donc faire des compromis quelque part. Il existe de très nombreuses façons différentes de faire un tel compromis, et je ne les détaillerai pas ici. Mais depuis environ deux cent cinquante ans, nous avons opté pour un système de réglage appelé Equal Temperament . Dans ce système, vous commencez par une hauteur de référence (par exemple A440), puis la fréquence de chaque autre note est de 2 ^{n / 12} , où n est le nombre de demi - pas au-dessus du pas de référence.

Dans ce système, aucun des intervalles n'aura de rapport de nombres entiers. Mais tous les intervalles sont cohérents (certains diraient toujours imparfaits), ce qui vous permet de jouer sur n'importe quelle touche. C'est un compromis efficace, mais vous perdez la pureté des véritables intervalles de rapport de nombres entiers. Et donc la réponse courte que j'ai donnée ci-dessus s'avère être seulement en quelque sorte correcte, car les intervalles de consonnes auront des rapports qui sont presque , mais pas en fait, de jolis petits rapports de nombres entiers.

Oui, il y a un moyen. Il y a des recherches brillantes de Norman D Cook qui portent spécifiquement sur les propriétés acoustiques des triades. Ce qu'il fait, c'est additionner divers partiels de trois tons quelconques et les mapper sur un espace tridimensionnel. Pour faire tenir les triades sur un espace 2D, il calcule la différence d'intervalle entre la première et la deuxième note, et met cela sur un axe, la différence entre la deuxième note et la troisième sur l'axe des y. Il effectue ensuite les calculs mathématiques pour diverses propriétés telles que la consonance, la tension, la modalité et l'instabilité. Il place cela sur ce qu'il appelle la grille triadique, où M représente la triade majeure, m pour mineur, s pour sus et a pour augmenté. Cette théorie modélise la façon dont nous percevons ces accords dans l'ordre dans lequel nous savons qu'ils sont consonnants, mais que jusqu'à présent nous n'avons pas réussi à expliquer mathématiquement. http://www.res.kutc.kansai-u.ac.jp/~cook/PDFs/MusPerc2009.pdf

Le papier est assez dense, si vous êtes pas dans les mathématiques et la théorie musicale, je suggérerais de regarder cette vidéo de lui discutant de sa théorie. C'est révolutionnaire, je pense, car cette réponse a, je pense, échappé à tout le monde jusqu'à présent. Il semble que cela devrait être basé sur la façon dont les ratios agissent purement mathématiquement, mais c'est en fait plus complexe que cela, d'où pourquoi il l'appelle un modèle psychophysique de perception de l'harmonie.

juste quelques commentaires supplémentaires:

1. Pour calculer une mesure de dissonance, il faut prendre en compte les harmoniques, c'est-à-dire calculer toutes les contributions par paires à la mesure et les résumer (pas trop difficile à faire).
2. Pour les accords de plus de deux hauteurs, vous résumez simplement toutes les contributions par paires à la mesure, aux fondamentaux et aux harmoniques.
3. La dissonance diminue avec la distance: l'équivalence d'octave ne fonctionne pas vraiment dans ce cas le respect. Une seconde mineure est plus dissonante qu'un neuf mineur qui est à son tour plus dissonant qu'un mineur 17.

Prenez toute la théorie avec un grain de sel. Vous pouvez aimer les piments forts ou détester les piments forts.

Vous pouvez penser que le 7ème accord majeur (par exemple CEGB) qui termine de nombreuses compositions de jazz et "La Création du Monde" de Darius Milhaud est la plus belle consonance imaginable, beaucoup plus intéressant qu'une simple triade. Ou vous pensez peut-être que c'est la dissonance la plus horrible.

La consonance et la dissonance peuvent être définies objectivement, comme vous le voyez dans les autres réponses, mais la plupart des gens les considèrent comme des termes subjectifs. En tant que tels, ils dépendent des oreilles, du goût et de l'histoire de l'auditeur.

Je répondrais à cette question du point de vue de la théorie musicale pure, plutôt que du point de vue du traitement du signal ou de l'EE ou de l'ingénierie audio. Le problème lorsque vous empruntez cette route (IMO) est que vous entrez dans toutes sortes de signaux qui peuvent être observés sur un oscilloscope, ou que vous passez par une FFT, qui ne sont pas du tout musicaux, cela pourrait être le son du métal. métal hurlant d'un wagon sur les voies. En termes musicaux, toutes sortes de demi-tons qui ne se trouvent pas sur l'échelle diatonique ou chromatique.

Du point de vue de la théorie musicale, la dissonance est mesurée par la quantité de notes ALTERED dans l'accord. Les notes modifiées sont simplement le b5, le n ° 5, le b9 et le n ° 9. En do majeur, ce sont respectivement Gb, G #, Db et D #. Notez que ce sont tous un demi-pas au-dessus et en dessous du 5 et de la tonique (fondamentale) de l'accord. La racine et le 5 sont les notes les plus consonantes, donc en jouant des notes à seulement 1/2 pas, nous obtenons le son dissonant.

Allez sur un piano ou une guitare et jouez un accord en utilisant uniquement ces notes - G, C #, G #, C - le 5, b9, # 5 et la racine, en hauteur croissante. C'est à peu près aussi dissonant que vous voudrez l'entendre.

Vous avez écrit "Chord", mais vous n'avez parlé que de deux combinaisons de notes, et la réponse est déjà marquée. N'oubliez pas non plus que nous parlons de musique ici. Ce qui est mesuré n'est pas le ton physique mais la perception de l'auditeur.

Je voulais néanmoins répondre que pour les 'vrais' accords à trois membres ou plus, le calcul simple ne s'applique plus. La composante psychologique devient plus importante. Un accord augmenté (c e g #) est une consonance (imparfaite) pour toutes les combinaisons, mais il est perçu comme l'un des accords les plus dissonants.

Aussi pour les combinaisons de deux notes, il importe dans quelle octave vous les jouez. Les intervalles dissonants sont moins dissonants si vous les jouez à une octave d'intervalle tandis que les intervalles de consonnes sont moins consonnantes lorsqu'ils sont joués séparément, les deux effets psychologiques.

Il y a d'autres paramètres autres que la hauteur qui peuvent prendre le dessus. Même avec juste des intervalles de réglage sur l'extrémité inférieure de notre spectre auditif, le son n'est pas aussi «bon» que dans la plage médiane. Notre oreille n'est pas linéaire, elle a ses bandes préférées dans le spectre audio, là où se trouve la langue parlée.