Une option si vous êtes principalement intéressé par la représentation des chiffres individuels de pi est d'utiliser une représentation dans une base autre que 10. Par exemple, pi base 12 aurait un numérique individuel pour chaque chromatique note.

Voici un site Web qui pourrait vous aider à démarrer: http://www.virtuescience.com/pi-in-other-bases.html

Le nombre 10 ne correspond pas nécessairement aux valeurs de la théorie musicale traditionnelle. (Par exemple, il y a 12 hauteurs chromatiques par octave, en utilisant des divisions conventionnelles de l'octave; les échelles diatoniques ont sept hauteurs; les durées des notes sont liées comme des puissances ou des puissances négatives de 2). Donc, pour cette raison, le monde est votre huître! Je suppose que vous pouvez choisir n'importe quelle 10 valeurs à mapper aux 10 chiffres.

Cela signifie qu'il est peu probable que vous obteniez une réponse définitive (et donc certains peuvent considérer ce post comme être hors sujet), mais voici quelques-unes de mes propres suggestions de mappages appropriés:

1. Divisez une octave par dix (c'est-à-dire utilisez 10-TET) bien que ceci youtube le clip suggère que quelqu'un vous a peut-être battu…!
2. Utilisez 10 accords différents.
3. Utilisez 10 durées de notes différentes (qui peuvent être liées soit par des puissances de 2, soit par des dixièmes de une valeur particulière).
4. Utilisez une paire d'échelles pentatoniques imbriquées (j'aime cette idée, peut-être séparée en stéréo, mais ce n'est pas mon projet…)
5. Utilisez une combinaison des idées ci-dessus , par exemple. différentes fréquences ont chacune leur propre durée associée (et leur positionnement stéréo…)

Au final, j'ai trouvé ces idées très rapidement, les possibilités sont vastes , et l'expérimentation est la clé.

INFORMATIONS SUPPLÉMENTAIRES: Si vous essayez de trouver les fréquences dans l'accord 10-TET, vous multiplierez une fréquence de départ par 2 à la puissance de n / 10, où n est un entier valeurs comprises entre 0 et 9.

Pi peut également être exprimé à travers diverses séries infinies. J'aime la série de François Viète découverte en 1593:

La racine carrée de 2 est une distance d'une demi-octave. Peut-être est-il possible de représenter la série comme une séquence de sons? Ou peut-être qu'une autre série conviendrait mieux? Cela pourrait reproduire l'esprit de Pi encore mieux que de rejouer sa représentation décimale.

Une idée que je n'ai pas vue mentionnée est le rythme. Vous pouvez peut-être utiliser certains des chiffres de réserve pour changer le rythme (par exemple, passer des huit aux croches). Ou vous pouvez mapper les chiffres de réserve à des motifs rythmiques préconçus.

Une autre idée serait d'utiliser les chiffres qui ne sont pas mappés à une note pour changer d'instrument.

HTH.

Pourquoi utiliser la base 10? Vous devez faire un compromis quelque part, et comme π est déjà transcendantal, il n'y a pas de base rationnelle qui représentera exactement π. Si vous utilisez heptaire, π ≈ 3.0663651432036134110263402244652226643520650240155443215426431025161154565220002622436103301443233631 . Ces chiffres correspondent parfaitement aux sept hauteurs d'une octave. Utiliser octal ajouterait soit un b3 , b7 , ou # 4 . Quintaire donnerait une gamme pentatonique parfaite.

Si vous voulez faire un beau morceau de musique (ce que je suppose que vous faites, encoder simplement pi serait un peu inutile), j'éviterais d'essayer de générer la musique mécaniquement, et utiliserais plutôt des morceaux de pi comme source d'inspiration.

Par exemple:

• L'écriture en 22/7 (une approximation de pi)
• En utilisant les 5 premiers chiffres comme motif dans d'une manière ou d'une autre, et en utilisant moins les autres. Vous pourriez alors avoir une cinquantaine de chiffres supplémentaires sous forme de section de type cadence rapide.
• Utilisation de progressions d'accords cycliques (pi représentant des cercles)

Une option que personne n'a vraiment mentionnée est d'utiliser ces chiffres supplémentaires à des fins spéciales (par exemple, changer le tempo, un autre instrument). Si l'instrument principal est un piano, j'imagine que le simple fait d'assigner un chiffre à la caisse claire, à la basse et à la cymbale ajouterait beaucoup de flair à votre musique finale.

En fait, l'ajout de nouveaux instruments ouvrira vous propose un tas de nouvelles façons de le faire. Vous pouvez laisser chaque chiffre représenter une opération. Chaque opération pourrait représenter un changement d'instrument, de tempo ou d'effet, etc ... De plus, chaque opération lirait alors autant de chiffres supplémentaires que nécessaire pour satisfaire son nombre de paramètres. Cela permettra à vos battements d'avoir des choses comme le sustain, l'accent, etc. pour vos notes.

Cela rendra en fait le problème d'avoir plus d'espace de données que d'espace de note encore plus un problème, sauf pour le fait que ce n’était jamais vraiment un problème au départ. Remplissez simplement l'espace supplémentaire avec les octaves supérieures et inférieures suivantes. Cela entraînera un léger déséquilibre des notes mais nous ne voulons pas vraiment d'équilibre de toute façon ...

Ce qui nous amène à un autre problème. Je pense que votre meilleur pari est d'utiliser des motifs trouvés dans la musique populaire pour vous assurer que la dispersion de vos notes est agréable. J'ai trouvé ce site qui contient les données que nous souhaitons pour déterminer que:

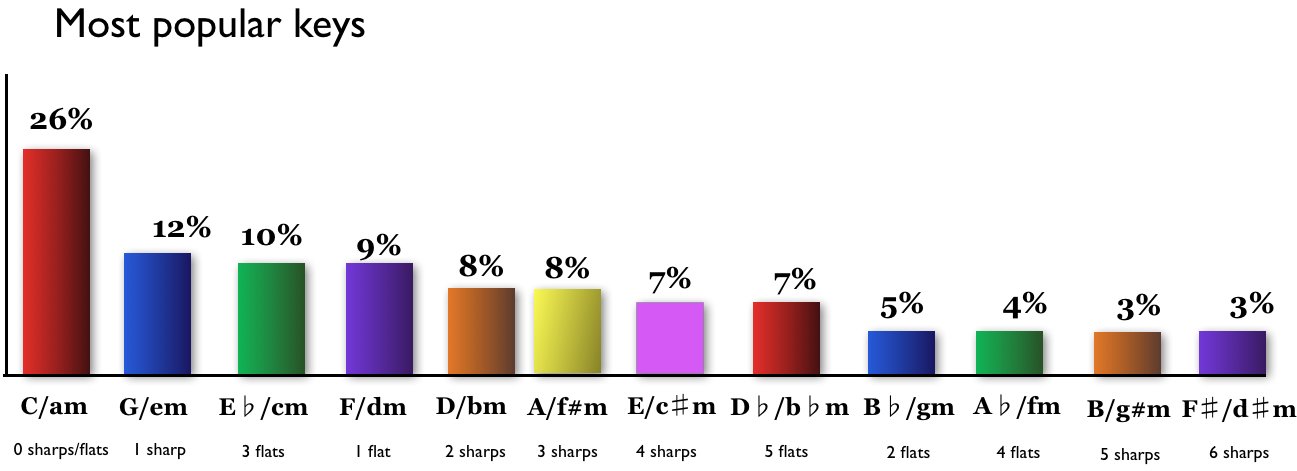
Votre application aura plus de chances de mieux sonner lorsque il produit des notes avec un modèle de dispersion similaire à celui-ci. Vous constaterez peut-être que certains instruments peuvent fonctionner très différemment, donc (comme pour tout cela) l'expérimentation sera importante.

Une fois que ce système fonctionne, je vous suggère d'essayer de penser à une autre chanson qui sonne similaire à ce que vous avez et fait un graphique de dispersion des notes plus exact qui correspond en fait à une chanson dans la même tonalité. Lisez la page sur le lien ci-dessus pour voir ce que je veux dire.

Si vous vouliez l'intensifier, vous aurez la possibilité d'ajouter autant de fonctions que vous le souhaitez. Il vous suffit de décider de la taille d'un code d'opération (1, 2, 3 caractères) en fonction du nombre de fonctions différentes que vous avez et de les gérer toutes (même si de gros blocs font la même chose). Si vous voulez vraiment que ce soit une symphonie complexe, je vous suggère de séparer l'étape de traitement de l'étape de lecture pour éliminer tous les problèmes de synchronisation que vous rencontrerez en raison du débit de données variable inhérent à une telle conception. Heureusement, il existe des normes. Un standard populaire est appelé MusicXML. Si vous créez votre programme pour générer simplement ces fichiers. Ensuite, vous pourrez lire ces fichiers ultérieurement à l’aide d’un lecteur MusicXML.

Mise à jour: si vous souhaitez voir mes expériences avec cela, vous pouvez obtenir ici.

Il n'y a aucune raison pour que vous restiez à moins d'une octave. Vous pouvez utiliser, par exemple, C-D-E-F-G-A-B-c-d-e pour vos chiffres. Ainsi, les cinq premières notes sont E-C-F-C-G-d, par exemple.Cela a l'avantage d'être extrêmement intuitif pour n'importe quel musicien, puisque vous vous référez simplement aux degrés d'échelle en do majeur (10 étant 0). Personnellement, je peux simplement m'asseoir là et lire les notes et les jouer sans y penser.

Avec la touche mineure que vous utilisez, vous pouvez également emprunter au majeur, ala le mineur harmonique. Ensuite, vous pouvez utiliser A-B-C-D-E-F-F # -G-G # -a. Ce n'est pas aussi intuitif, mais cela produit des effets intéressants, sans paraître complètement chromatique. Les premières notes deviennent C-A-D-A-E-G # -B-F-E-C-E G-G # -F # -G # -C-B-C-G-D-F B-F-D-C-C-G-C-B-F # -G # -E-a. Ce dernier bit ressemble à une cadence réelle.

En tant que programmeur, j'adore cette idée et bien sûr j'y ai déjà pensé mais je n'ai pas encore eu le temps de l'essayer :).

En gros, je crois que votre ligne avec les notes sont incorrectes. Vous devez commencer par choisir une clé dans laquelle vous souhaitez l'écrire. Je crois que votre clé serait Am, ou est-ce une coïncidence? Je travaillerais avec quelque chose comme ceci:

 char notes [] = {'A', 'B', 'C', "D", "E", "F", "G"}; String pi = String.valueOf (Math.PI); pour (int i = 0; i < pi.length (); i ++) {char currentChar = pi.charAt (i); if (currentChar! = '.') {// nie le didigt décimal System.out.println (currentChar); char currentNote = notes [(Integer.parseInt (currentChar + "") - 1)% notes.length]; System.out.println (currentNote); }} 

Notez qu'il s'agit de Java.

EDIT: Ce code est conçu de telle sorte que si vous avez un nombre plus grand que le nombre de notes fournies, il recommencera à partir de la première note. Donc 8 serait la note de retour 0 (A).

D'autres réponses suggèrent d'utiliser différentes bases. Pour un événement dans le département de physique, j'ai joué à pi en quintal, et il y a une vidéo. La feuille a été générée en utilisant un script et Lilypond.

Bonus: également en octal, mais celui-ci n'est pas annoté.

Voici une autre idée, bizarre même selon mes critères. Pour ceux qui ne connaissent pas la règle de composition à 12 tons (comme indiqué à l'origine; probablement changé plusieurs fois), il est dit que vous ne pouvez répéter aucune tonalité tant que les 11 autres n'ont pas été jouées. Les accords en série ou en accords sont autorisés.

Voici donc la règle de composition "12 tons pi": pour chaque chiffre de pi, vous êtes autorisé à sauter autant de tons au cours des 12 prochains cycles. Par exemple, le premier cycle n'a besoin que de 9 (12-3) tonalités avant de se répéter; le cycle suivant a besoin de 11 (12-1) tons, et ainsi de suite.

Des points bonus si vous pouvez faire en sorte que le morceau ne ressemble PAS à Webern ou Berio :-)