Le résumé le mieux écrit que j'ai pu trouver à ce sujet était sur Wikipédia.

Préliminaires techniques (vous pouvez sauter ceci si vous ne vous en souciez pas)

Tous les chordophones (instruments de musique basés sur des cordes vibrantes) peuvent être analysés en utilisant le même modèle physique d'une corde sous tension fixée aux deux extrémités. Le modèle est légèrement simplifié et diffère de la réalité de deux manières: dans le modèle, la corde a une épaisseur nulle et la corde a une rigidité nulle. Lorsque l'on compare les résultats calculés sur la base du modèle avec le comportement réel de ces chaînes, il s'avère que ces deux simplifications ne font pas de différence significative dans la plupart des domaines. Une exception à cela est que le besoin d'un accordage extensible sur certains instruments comme le piano n'est pas prédit par le modèle en raison de l'omission de la rigidité.

La discussion suivante sera basée sur le modèle de mouvement des cordes décrit au dessus. Lorsque la corde est au repos, aucun son n'est produit. Lorsque la position de la corde est perturbée, par pincement, frappe, etc., la tension sur la corde agit pour ramener la corde dans sa position de repos. La masse de la corde donne à la corde l'inertie qui fait que la corde dépasse sa position de repos et se déplace à nouveau dans la direction opposée, et à nouveau la tension agit pour restaurer la corde en position de repos, etc. La tension et la masse interagissent de cette manière pour faire avancer et reculer la corde jusqu'à ce que quelque chose arrête le mouvement de la corde. Une corde qui n'est pas intentionnellement amortie finira par s'arrêter en raison du frottement qui convertit l'énergie cinétique de la corde en chaleur.

La formule (c'est la réponse mathématique à votre question)

Dans notre modèle et dans les chaînes du monde réel, le mouvement de va-et-vient de la chaîne perturbée se stabilise rapidement à une fréquence de résonance . Cette fréquence est déterminée par les propriétés de la chaîne, et basée sur le modèle peut être calculée (avec une précision raisonnable) par l'équation suivante:

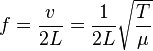
Où :

• f est la fréquence de résonance (la note jouée)
• v est la vitesse de propagation d'une perturbation (onde) sur la longueur de la string
• L est la longueur de sondage de la chaîne (la longueur entre les deux points fixes à chaque extrémité de la partie perturbée de la chaîne)
• T est la tension de la corde (le long de la longueur de sondage, si la tension n'est pas partout la même)
• mu est la densité linéaire , ou masse par unité de longueur

Notez que la fréquence de résonance ne dépend pas de la masse totale de la corde le long de la longueur de sondage. Dans le modèle et la formule, la composante de longueur qui serait multipliée par mu pour obtenir la masse totale «s'annule», donc c'est seulement la densité linéaire qui compte.

Les conséquences musicales (lire au moins ceci )

Le modèle et la formule que nous avons créés pour nos cordes vibrantes suggèrent les choses suivantes pour changer la fréquence de résonance (et donc la note que nous jouons) de nos cordes:

• Pour jouer une note plus haute, on peut réduire la longueur, réduire la densité linéaire (en pratique, l'épaisseur), ou augmenter la tension d'une corde.
• Pour jouer une note plus basse, on peut augmenter la longueur, augmentez l'épaisseur ou diminuez la tension sur la corde.

Comme mentionné ci-dessus, une fois que notre modèle atteint le monde réel, nous rencontrons rapidement un problème: l'épaisseur des cordes (qui est ignorée dans le modèle) est le moyen le plus simple de contrôler la densité linéaire, mais a des effets sur le final ton et accord de l'instrument de musique. Plus la corde est fine, plus la corde réelle est proche du modèle (puisque le modèle suppose une épaisseur nulle), ce qui facilite les calculs de construction de l'instrument. D'autre part, les cordes plus épaisses ont tendance à avoir un ton plus riche (citation nécessaire - subjective). D'un autre côté, les cordes plus épaisses ont également une plus grande rigidité, ce qui s'écarte davantage du modèle et pose d'autres problèmes (à part: c'est l'une des raisons pour lesquelles les cordes plus épaisses sont fabriquées à partir de fil enroulé autour du fil, plutôt que juste en utilisant un morceau de fil solide vraiment épais. Les cordes enroulées sont beaucoup moins rigides que les cordes pleines de même densité linéaire.) Il y a aussi des problèmes compliqués concernant l'adaptation d'impédance mécanique entre les cordes et les ponts ou les points fixes, etc., ce que j'ai gagné '' Plongez-vous profondément ici.

Avec un peu d'expérimentation, nous pouvons trouver une épaisseur et une composition de cordes idéales pour tout instrument donné utilisant des cordes. Mais maintenant, nous commençons à avoir d'autres problèmes. Si nous fixons l'épaisseur (densité linéaire) de toutes les cordes de notre instrument, alors la seule façon de changer les notes jouées par ces cordes est de changer la longueur et / ou la tension. La tension peut être un problème car les matériaux que nous utilisons pour étirer les cordes doivent être suffisamment solides pour résister à cette tension. C'est pourquoi les cadres de piano en fonte étaient importants lors de leur introduction. En revanche, les cordes trop lâches n'auront pas une tonalité ou une intonation aussi bonne. La longueur est un problème car encore une fois, il y a des problèmes de construction d'instruments ainsi que de jouabilité. Pour un instrument comme la guitare, il n'est pas pratique de faire en sorte que les cordes aient différentes longueurs de son non frettées. Pour un instrument comme le piano, la longueur idéale des cordes les plus basses serait extrêmement longue. Même un piano à queue de 9 pieds est un compromis sur la longueur!

Réalités de la construction du piano

Avec le piano, il y a une excellente occasion d'équilibrer l'épaisseur, tension, et longueur des chaînes, car chaque note a sa ou ses propres cordes! Plus ou moins, les pianos modernes sont construits pour essayer d'avoir la longueur, la tension et l'épaisseur optimales pour chaque note, mais il y a beaucoup de défis et de compromis à faire.

Des cordes plus fines avec des longueurs sonores plus courtes peuvent jouer le bon note, mais ils sont aussi plus silencieux et ont un sustain plus court. C'est pourquoi si vous regardez les notes aiguës du piano, vous verrez trois cordes utilisées pour chaque note. Cela n'aide pas beaucoup avec le sustain (notez que les étouffoirs sont entièrement omis pour les notes les plus élevées de nombreux pianos) mais cela aide à uniformiser le volume.

Des cordes plus épaisses aident à réduire la note produite par une corde, mais nous avons alors des problèmes de rigidité. Nous avons également besoin d'une certaine tension pour éviter que la corde ne soit "trop ​​souple" (terme technique). Alors faisons les notes de basse sur le piano vraiment longues! Eh bien, cela pose des problèmes pour installer le piano dans un salon ou sur une scène bondée et rendre le piano très cher. Les orchestres symphoniques peuvent se permettre de prendre beaucoup de place et d'argent sur les meilleurs pianos, vous pouvez donc voir des grands de concert de 9 pieds de long joués pour des concertos. À la maison, vous pourriez avoir une épinette avec une longueur de sondage maximale de seulement environ trois pieds et un son de basse moins riche pour aller avec ça.

Donc, trouver l'équilibre idéal entre longueur, tension, épaisseur, la tonalité, le coût et la taille sont tous des facteurs qui déterminent la longueur de chaque corde sur un piano donné.

Réalités de la construction de la guitare

Sur une guitare, les cordes ont toutes pour avoir approximativement la même longueur. Si ce n'était pas le cas, ce ne serait pas une guitare et elle ne pourrait pas être jouée comme une guitare. Chaque corde doit également avoir à peu près la même tension, sinon la tension mal adaptée sur les cordes peut éventuellement déformer la guitare et détruire sa sonorité et son intonation. Cela signifie que l'épaisseur est notre principal outil pour créer les notes de cordes ouvertes sur une guitare.

Cela nous amène à une différence fondamentale entre la guitare et le piano. Chaque note du piano a sa ou ses propres cordes, tandis que chaque corde de la guitare est utilisée pour jouer plusieurs notes. Il n'est pas pratique de changer l'épaisseur ou la tension d'une corde en temps réel pour jouer de la musique, donc sur la guitare (et tous les instruments de la famille des cordes), différentes notes sont jouées sur la même corde en changeant la longueur sonore de la corde .

Ainsi, même si les longueurs de sons "ouvertes" de base de toutes les cordes d'une guitare (ou d'un violon ou d'un violoncelle, etc.) sont les mêmes, pendant qu'elle est jouée, les longueurs de son sont toutes changeantes et potentiellement très différentes. Au cas où cela ne serait pas évident, la longueur des cordes sur la guitare est modifiée par fretting , c'est-à-dire en appuyant sur la corde contre une barre de métal (qui est placée dans un emplacement particulier) qui agit pour raccourcir la longueur de sondage de la chaîne.

Résumé

C'est donc moyen d'avoir trop d'informations pour dire simplement: C'est la longueur, la tension, et l'épaisseur combinée qui déterminent la ou les notes faites par une corde. Sur un piano, ceux-ci sont tous pré-choisis et accordés avant qu'une seule touche ne soit frappée. Sur une guitare, l'épaisseur et la tension sont pré-choisies, ainsi que six longueurs de base, puis les longueurs sont modifiées dynamiquement pendant la performance.

Le diamètre de la corde, la longueur et la tension de l'échelle sont tous des facteurs, mais vous oubliez une dimension totalement différente de votre question.

Frettes.

Une corde de guitare a une longueur fixe, mais avez-vous remarqué les frettes? Lorsque vous arrêtez une corde contre une frette, vous créez alors temporairement une longueur de corde parlante plus courte. Ainsi, une corde sur une guitare peut être arrêtée dans 19 positions de frette différentes, ce qui équivaut à avoir 20 longueurs de corde différentes formées à partir d'une seule corde. Donc, dans ce sens pratique de la manière dont les notes sont jouées sur l'instrument, il n'est pas correct de dire qu'il n'y a qu'une seule longueur de corde sur une guitare.

Le piano, en revanche, est un instrument à clavier et n'utilise pas de frettes. Chaque hauteur différente est déclenchée indépendamment par une touche différente frappant des cordes ouvertes, de sorte que chaque touche doit avoir son propre jeu de cordes accordé à une hauteur fixe. Donc, pour jouer ces mêmes 19 hauteurs à partir de la corde de guitare sur un piano, vous avez besoin de 19 groupes séparés de cordes de piano.

Pouvez-vous imaginer tout cela? Plus précisément, procurez-vous une guitare et un piano, jouez-les et observez leur fonctionnement. En parler dans l'abstrait n'est pas très utile, mais mettre la main dessus et les jouer l'est.

En fait, il y avait un clavier historique appelé le clavicorde (dans les années 1600) qui avait des frettes. (en fait, on les appelle tangentes , mais elles fonctionnent comme des frettes sur une guitare.) C'était une sorte d'hybride entre le piano et la guitare. Certains clavicords auraient, par exemple, 36 clés mais seulement 18 paires de chaînes, car une clé frapperait une paire de chaînes à une longueur, tandis que la clé adjacente frapperait la même chaîne mais l'arrêterait à une longueur de parole différente (ou frette, pour ainsi dire). Le résultat de ceci est que certains accords que vous pouviez jouer sur un piano ne pouvaient pas être joués sur un clavicorde, car il n'y avait pas beaucoup de cordes disponibles pour jouer toutes les notes de l'accord. Ceci est analogue à la situation sur la guitare, qui n'a que six cordes à partir desquelles former un accord donné.

La hauteur que produit une corde est déterminée par la fréquence de vibration de la corde. En d'autres termes, à quelle vitesse vibre-t-il. Le taux de vibration d'une corde lorsqu'elle est pincée ou frappée dépend de plusieurs facteurs.

La tension de la corde n'est que l'une des choses qui affecteront la fréquence . Une corde placée sous une tension plus élevée vibre plus rapidement et la hauteur que vous entendez sera plus élevée que la même corde avec moins de tension. Sur un piano et une guitare, la hauteur des cordes est réglée finement en serrant les cordes jusqu'à ce que la fréquence désirée soit émise lorsque la corde est excitée.

La longueur d'une corde à une tension donnée affectera également la fréquence. Plus une corde donnée est courte à une tension donnée, plus elle vibre rapidement lorsqu'elle est jouée. Sur un instrument comme la guitare, appuyer sur la corde contre le manche derrière diverses frettes augmentera la hauteur de la note jouée par la corde en raccourcissant la corde et en la faisant vibrer à une fréquence plus élevée.

Le diamètre de la corde affectera également la fréquence à laquelle elle va vibrer à une tension donnée. Les cordes de plus grand diamètre vibreront plus lentement et produiront un son de fréquence plus basse que les cordes plus fines.

Enfin, la densité du matériau dont la corde est faite affectera la vitesse à laquelle elle vibre à une tension donnée. Ainsi, une corde d'acier sur une guitare vibre à une vitesse différente d'une corde en nylon sous la même tension.

En utilisant une guitare à six cordes pour illustrer, oui, nous commençons avec six cordes de longueur relativement égale. Mais chaque corde a un diamètre différent qui affecte la fréquence à laquelle la corde va vibrer sous une tension donnée. Un jeu de cordes de guitare sera dimensionné de sorte que la tension soit relativement uniforme dans l'accord standard sur les six cordes. Mais la corde de mi bas sera beaucoup plus épaisse que la corde électronique haute et sera également faite d'un matériau avec une densité différente qui vibrera également plus lentement en raison d'une plus grande masse.

Lorsque vous raccourcissez les cordes en frottant des notes sur le manche, vous les faites vibrer à une fréquence plus rapide et jouez des notes plus hautes. Vous avez 6 cordes qui jouent chacune une note différente. Mais chaque corde d'une guitare acoustique standard peut jouer 20 notes différentes en raccourcissant la corde avec vos doigts de frottement.

Sur un piano, vous avez besoin de 88 fréquences différentes. Et vous ne pouvez pas raccourcir les cordes avec vos doigts comme vous pouvez le faire sur une guitare. Ainsi, chaque corde doit être accordée pour vibrer à la fréquence appropriée qui correspond à chaque touche du piano. Différentes longueurs de corde en combinaison avec différents diamètres de cordes et matériaux sont utilisées sur le piano pour accorder de manière optimale chaque touche à la bonne note sans avoir besoin de trop de tension. Tout comme la guitare, les cordes de basse d'un piano sont plus épaisses - elles n'ont donc pas besoin d'être aussi longues pour vibrer à la fréquence lente requise.

Vous pouvez donc modifier la hauteur de la note créée par une corde vibrante en augmentant ou en diminuant la tension et / ou en modifiant la longueur. Mais pour garder la taille de nos instruments gérable, la meilleure approche consiste à utiliser une combinaison de tension, de longueur, de diamètre et de matériau pour maintenir un équilibre optimal sans tension excessive qui pourrait endommager l'instrument.

La longueur et la tension travaillent ensemble pour créer la hauteur. Notez que les cordes d'une guitare sont toutes à peu près de la même longueur et de la même tension, mais le fond fait environ 4/5 fois le diamètre de la corde supérieure. Sur n'importe quel instrument à cordes, il est important que chaque corde ait à peu près la même tension que les autres, de sorte que cela devienne statique dans une certaine mesure. Les deux variables sont donc l'épaisseur (essentiellement l'épaisseur) et la longueur. Plus la jauge est grande, plus une corde donnée doit être courte pour produire une note particulière.

À la guitare, la longueur de la corde dépend à peu près de la longueur de la guitare, pour être jouable. Une basse aura des cordes à la fois plus longues et plus épaisses. Au piano, il y a plus de marge de manœuvre - les cordes peuvent être verticales ou trop cordées, car il y a plus de place. Donc, dans une certaine mesure, il est plus facile d'accommoder des cordes plus longues / plus courtes au piano qu'à la guitare.

J'espère que quelqu'un développera cela avec des chiffres scientifiques, mais pour l'instant, c'est une explication profane.

La formule est

fréquence = sqrt (tension / masse par unité de longueur) / (2 * longueur)

Le facteur de 2 provient de le fait qu'une vibration fondamentale harmonisée doit parcourir toute la longueur de la corde et remonter pour être en phase.

Vous pouvez jouer avec tous les paramètres. Une guitare a 6 cordes à peu près de la même tension, mais d'épaisseur différente. Cela permet une différence de 2 octaves entre les cordes les plus lourdes et les plus légères. Fretting la corde à la 12e frette divise par deux la longueur de la corde, double la fréquence et augmente la hauteur d'une octave. Certaines guitares électriques ont 24 frettes, ce qui signifie qu'elles peuvent jouer une plage de 2 octaves sur une seule corde en réduisant la longueur de parole à un quart. La plage totale est donc 2 + 2 = 4 octaves. Il est également possible (mais très inhabituel) d'avoir une guitare basse combinée dans le même instrument, ce qui ferait un total de 5 octaves.

Cela pose cependant des problèmes. Pour avoir la même échelle qu'une guitare ordinaire, les cordes de guitare basse devraient être très lâches ou très épaisses, ce qui rendrait l'instrument difficile à jouer. Par conséquent, les guitares basses ont une gamme plus longue que les guitares ordinaires.

Le piano, par contre, utilise des variations de longueur et d'épaisseur beaucoup plus importantes et atteint une plage de 7 octaves.

Pour le vent instruments, la vitesse du son dans l’air est constante. Cela signifie qu'il y a moins de variables avec lesquelles jouer et qu'il est rare d'obtenir plus d'une octave et demie à partir des positions de doigté. La clarinette parvient à presser plus de 2 octaves de plus en utilisant des harmoniques, ce qui lui donne une plage de près de 4 octaves, ce qui est impressionnant, mais toujours moins que la plupart des guitares électriques.

Un point a été laissé de côté jusqu'à présent. La conception d'une guitare ne nous laisse pas d'autre choix que d'avoir des cordes de longueur égale avec une épaisseur différente (avec les frettes utilisées pour contrôler la longueur de toutes les notes sauf E-A-D-G-B-E pour une guitare à l'accord conventionnel). Un piano change à la fois de longueur et d'épaisseur: cela semble exagéré jusqu'à ce que vous vous rendiez compte qu'il y a le problème de l ' énergie et de l' intensité perçue du son - quelle est son intensité et combien de temps ça sonne? Pour qu'un piano sonne bien, vous aimeriez avoir la même intensité sonore lorsque vous appuyez sur les touches de la même manière, et vous aimeriez (si possible) que les cordes sonnent en même temps. Vous souhaitez également que les cordes sonnent de la même manière. Ce n'est pas vraiment possible, mais un piano, ayant un degré de liberté supplémentaire dans la conception, se rapproche beaucoup plus qu'une guitare.

Ce qui suit emprunte beaucoup à cet excellent article sur l'acoustique des pianos - Je vous recommande vivement de lire l'original plutôt que ce mauvais résumé. Cela vaut à la fois pour les figures, les équations et la théorie décrite.

Dans le chapitre 5, l'article traite de la relation entre la longueur l, la tension T, la masse par unité de longueur λ et la fréquence f - donnant

Si vous avez deux cordes avec des fréquences distantes d'une octave, vous pouvez en principe obtenir cette différence en changeant un seul des facteurs - la longueur , tension ou masse. En pratique, il est souhaitable de les changer tous. Le changement de fréquence est le produit du changement de longueur, du changement de diamètre et de la racine carrée du changement de tension:

Maintenant si vous voulez que toutes les notes aient à peu près la même tension, vous voudriez que les cordes aient le même diamètre - mais cela signifierait, sur la plage d'un piano, un changement massif de longueur ou de diamètre pour compenser. Donc, à la place, les cordes deviennent un peu plus longues et un peu plus épaisses, et ont une tension légèrement inférieure, à mesure que nous descendons en fréquence.

Mais il y a un facteur supplémentaire important: la rigidité de la corde. Là où une corde «parfaite» se plierait facilement, de sorte que seule la tension détermine la fréquence et la propagation des ondes, dans une corde en acier il y a un certain mode de propagation du son dû simplement à la rigidité de la corde. Cette rigidité affecte davantage les harmoniques supérieures - et a un impact plus important sur les cordes courtes et haute tension en haut de gamme.

En principe, les cordes inférieures, étant plus longues, souffrent moins de ce problème ; mais pour des raisons pratiques, les notes les plus basses ont des cordes plus courtes pour garder la taille du piano "raisonnable".

Mais voici une chose amusante. L'oreille humaine ne peut pas très bien entendre la hauteur des notes les plus graves sur un piano - à la place, nous utilisons le contenu harmonique pour «deviner» la fondamentale. Cela rend les notes les plus basses sur une verticale (avec des cordes plus courtes à l'extrémité inférieure) un son moins agréable que les mêmes notes sur un piano à queue - qui a des cordes plus longues et donc des harmoniques mieux comportées. En fait, la longueur des cordes que l'on aimerait à l'extrémité inférieure dépasse même ce qui peut tenir à l'intérieur d'un piano à queue - de sorte que les cordes les plus basses sont plus courtes que ce que l'on pourrait souhaiter autrement (et à une tension plus faible) :

Enfin - la question du volume et de la décroissance. Le graphique suivant montre comment l'intensité du son diminue sur le clavier, les notes les plus basses étant maintenues plus longtemps:

Rendre les cordes inférieures plus lourdes a pour effet de les faire «sonner» plus longtemps; mais il est aussi plus difficile de leur donner un gros coup de pied - afin qu'ils donnent une intensité plus similaire pour le même toucher sur le clavier.

Dans l'ensemble, un piano est un instrument extrêmement complexe. En revanche, une guitare est beaucoup plus simple.

La longueur et le facteur de tension dans la fréquence d'une corde vibrante, ainsi que la masse de la corde. Les raisons des différences proviennent de la façon dont on joue des instruments et de la physique.

Dans le cas de la guitare, les accords sont joués en utilisant les doigts pour pousser les cordes vers le bas sur les frettes, ce qui diminue la longueur de la chaîne. Cela montre que les cordes de guitare "changent de longueur" pour créer des accords, mais ne explique pas pourquoi les cordes sont toutes de la même longueur lorsqu'elles sont ouvertes. C'est une question de physiologie. Si les cordes haute fréquence étaient plus courtes, vous ne seriez pas en mesure d'atteindre vos doigts assez largement pour manipuler les cordes aiguës et graves en même temps. Il deviendrait impossible de jouer des accords.

Un piano est construit différemment avec une ou plusieurs cordes pour chaque note qui peut être jouée. Cela permet toutes sortes de sons qu'un piano peut créer qui ne peuvent pas être créés par une guitare, comme les accords avec de nombreuses notes. Rien dans la structure d'un piano n'empêche un accord Cmaj d'être joué simultanément sur 4 ou 5 octaves! Les pianos gagnent cette capacité en ayant suffisamment de cordes pour jouer simultanément chaque note du piano. Cependant, cela signifie également qu'il y a beaucoup plus de cordes tirant sur la table d'harmonie. Les forces sur un piano sont si grandes qu'il y a des plaques de fonte épaisses pour supporter la tension; le piano craquerait ou se plierait (et perdrait ainsi la mélodie) s'il n'était pas si fort! ¹ Essayer de faire toutes les cordes de la même longueur serait un exercice futile. Vous voudriez rendre les cordes hautes ultra-serrées. Les cordes de piano sont déjà proches de la résistance à la traction de l'acier de haute qualité! L'alternative serait de fabriquer des fils plus minces (pour diminuer leur masse), mais fabriquer des fils assez épais sur le bas de gamme et assez fins sur le haut de gamme serait un cauchemar des matériaux! Ils doivent déjà le faire pour les notes graves en enveloppant les cordes. Ce serait 10 fois pire s'ils ne variaient pas non plus la longueur.

Et bien sûr, ayant le parti pris d'un pianiste, je trouve que c'est plus joli comme ça ;-)

¹ Je ne suis pas un accordeur de piano, mais d'après ce que j'ai entendu, les forces sur un piano sont en fait suffisants pour fléchir la plaque en fonte sur laquelle les cordes sont attachées. Apparemment, ils fléchissent suffisamment pour que lorsque vous accordez certaines cordes, cela plie suffisamment la plaque pour en désaccorder d'autres. L'accord de piano est un véritable art!

Commencez par clarifier certaines idées fausses. Toutes les cordes d'une guitare ont en fait une longueur différente mais elles se ressemblent. Le chevalet sur le corps est légèrement incliné donc techniquement les cordes ont toutes une longueur différente:

La raison principale pour laquelle les cordes peuvent être environ la même longueur mais avoir des pas différents a à voir avec l'épaisseur de la corde. Sur un piano, vous voulez que chaque corde ait son propre son unique pour la note, vous devez donc varier l'épaisseur et la longueur et pas seulement l'une ou l'autre comme à la guitare.

Toutes les cordes de la guitare (ou des autres instruments à cordes à manche) sont différentes: elles ont des matériaux partiellement différents (les cordes inférieures ont tendance à être enroulées avec du fil) et elles ont certainement une épaisseur différente. Ils sonnent mieux à une tension particulière.

Vous les achetez généralement en sets même s'ils vieillissent différemment.

Les cordes de piano sont très durables et rarement changées: il n'y a pas de "sets" réels . Si un accordeur de piano devait transporter des cordes de remplacement séparées pour les 88 notes différentes, ce serait compliqué. Ainsi, le piano se débrouille avec beaucoup moins de cordes différentes, variant au lieu de cela leur longueur avec des hauteurs variables et ne passant qu'occasionnellement au type / épaisseur de corde suivant. De cette façon, un accordeur n'a besoin de transporter qu'un nombre limité de tailles de cordes de remplacement (les cordes basses inférieures ont un enroulement qui s'arrête avant les extrémités des cordes, elles doivent donc être dimensionnées individuellement après tout et ne peuvent pas être coupées sur place, mais il est beaucoup moins courant pour eux d'exiger des changements qu'avec les plus élevés).