La réponse liée est un peu désordonnée, et c'est un gâchis courant que les gens font.

Quand nous parlons des fréquences exactes de chaque classe de hauteur, nous devons connaître le tempérament, et un pas de référence. Par exemple, le tempérament égal 12 tons (12TET) avec A4 = 440Hz est une norme dans la musique moderne. À partir de ces deux paramètres, nous pouvons extrapoler la fréquence exacte de chaque note possible.

12TET est presque omniprésent de nos jours (du moins dans la musique occidentale), mais il ne sonne pas aussi propre que Just Intonation (JI) . En substance, 12TET a rendu chaque touche sonore tout aussi imparfaite. JI crée une gamme où les intervalles dans les accords primaires sont tous de très bons rapports simples, et ainsi les accords sonnent très clairement, mais cela ne fonctionne que dans cette tonalité. Note importante: dans un accord JI donné, chacune des 12 classes de hauteur n'a encore qu'une seule fréquence. Il n'y a pas de différence entre C♯ et D ♭ dans, disons, "Accordage pythagoricien basé sur A, avec A = 440Hz".

Mais la plupart de la musique ne reste pas dans une clé. Alors qu'un piano ne peut pas faire des ajustements de hauteur à la volée (c'est pourquoi nous avons accepté d'utiliser 12TET pour cela), la plupart des instruments d'un orchestre le peuvent. Ainsi, lorsque le morceau est en la majeur, l'orchestre utilisera JI et ajustera C♯ pour qu'il soit un peu plus plat qu'il ne le serait s'il utilisait 12TET. Mais alors si le morceau module en Fa mineur, ils commenceront à le jouer légèrement.

Quand les gens disent que C♯ n'est pas la même chose que D ♭, ce qu'ils veulent vraiment dire (s'ils le réalisent ou non) est-ce que le contexte peut conduire à différents micro-ajustements. En Do majeur, un Do pourrait être le tiers d'un accord de La majeur, peut-être une dominante secondaire de l'accord ii, tandis que D ♭ pourrait être la racine de l'accord napolitain. Cela entraînerait différents choix de réglage.

(modifié à partir des suggestions de commentaires, certains commentaires sont désormais orphelins)

La réponse courte est que pour le tempérament égal à 12 tons (12TET), le système d'accordage de facto pour la musique occidentale, Db et C # sont exactement la même note sonore . La fréquence exacte de cette note pour une octave donnée dépend également de la référence de hauteur, qui est généralement A4 = 440 Hz.

Selon 12TET, nous divisons l'octave en 12 rapports égaux. Puisqu'une octave est un rapport de 2: 1, le rapport d'une note f1 à la note 1 demi-ton plus haut f2 , est calculé comme f2 = f1 * 2 ^ (1/12) avec 2 ^ (1/12) ~ = 1.059463 .

Bien que ce soit de loin le système de réglage le plus courant que vous rencontrerez ( dans un contexte occidental au moins), il ne s'agit que d'une approche de réglage, et est relativement moderne par rapport à de nombreuses alternatives que vous pouvez rencontrer, y compris le système de Pythagore mentionné dans la question à laquelle vous avez fait référence (qui, comme son homonyme le suggère, a des milliers d'années) .

Le système d'accord de Pythagore adopte l'approche de la détermination de chaque note en calculant la quinte parfaite en utilisant le rapport de 3: 2, soit 1,5 fois la fréquence de référence. En plus d'être un rapport simple, ce système d'accordage est en fait très facile à mettre en œuvre car cette fréquence exacte (strictement 3: 1, une octave au-dessus de 3: 2) sera déjà présente dans la série harmonique de la note de référence pour la plupart des instruments de musique (instruments à cordes et à vent, y compris la voix humaine). C'est certainement le cas pour les violonistes, qui accordent leurs cordes (qui sont parfaitement espacées de quintes) par cette méthode.

Cependant, une quinte parfaite sous l'accord de Pythagore est d'environ 702 cents, contre exactement 700 cents en 12TET. Si vous continuez à régler de cette façon pour toujours vous n'atteindrez plus jamais le même ton . En vous réglant autour du cercle des quintes, vous construirez des fractions avec de plus grandes puissances de trois 3 ^ n sur de plus grandes puissances de deux 2 ^ m et il n'y a aucun moyen que fraction sera toujours égale à 1 (le pas de référence) sauf lorsque m = n = 0 , c'est-à-dire le pas de référence avec lequel vous avez commencé .

Si nous calculons les rapports de G (puisque G est la hauteur la plus éloignée de C # / Db dans les deux sens), monter en quintes ressemblerait à:

G -> D (3/2) -> A (9/4) -> E (27/8) -> B (81/16) -> F # (243/32) -> C # (729/64)

Si nous revenez dans l'autre sens (c'est-à-dire en descendant par quintes parfaites), cela ressemble à ceci:

G -> C (2/3) -> F (4/9) -> Bb (8/27) -> Eb (16/81) -> Ab (32/243) -> Db (64/729)

Si nous normalisons les fractions résultantes pour qu'elles se produisent dans la même octave, cela fonctionne pour être C # à 729/1024 ~ = 0.71191 vs Db à 512/729 ~ = 0.70233 , ce qui sera évidemment différent. J'ai calculé la différence entre ces notes à 23,46 cents, pas les 41 cents mentionnés dans la question référencée.

Pour mettre ces chiffres en perspective, si nous supposons que A est 440Hz, alors nous pouvons déterminer la référence G comme étant à deux cinquièmes parfaits à 8/9 x 440 ou ~ 391,11 Hz. En utilisant ce G, nous pouvons trouver les Db et C # de Pythagore directement en dessous de ce G en utilisant les ratios ci-dessus à ~ 274,689Hz et ~ 278,436Hz respectivement. Comparez cela à 12TET avec A4 = 440Hz, nous aurions G juste en dessous à ~ 391,995Hz et le Db / C # enharmonique à ~ 277,183Hz.

Il est peu probable que vous rencontriez une situation dans laquelle C # et Db sonnent réellement à 23,46 centièmes de distance pour un certain nombre de raisons. La première et la plus évidente raison est que 12TET est omniprésent dans les contextes musicaux occidentaux. La plupart des instruments à frettes modernes (guitares / basses) et des instruments à clavier (piano, orgue, etc.) sont accordés selon 12TET.

Même dans le cas rare où vous avez une collection de chanteurs exécutant a cappella, tel comme dans un quatuor de salon de coiffure, ils ne s'éloigneront probablement pas trop de l'accordage conventionnel grâce à la mémoire tonale. Fondamentalement, même les personnes sans hauteur parfaite peuvent avoir une certaine mémoire des notes de telle sorte que les systèmes d'accord plus `` naturels '', tels que Pythagorean, seront modifiés par leur mémoire des notes 12TET qu'ils ont probablement entendues toute leur vie.

Comme déjà dit,

• Le message que vous avez posé se réfère spécifiquement à C♯ et D ♭ dans le réglage de Pythagore .
• L'écart de 41 ct est faux, aucune idée de la façon dont cela s'est produit ^{Voir ci-dessous} .
• Le réglage de Pythagore n'est qu'un des multiples systèmes d'intonation juste.

Donc en fait, non seulement les notes C♯ et D ♭ sont différentes, mais il existe en fait plusieurs notes différentes que vous pouvez appeler C♯! Pour donner une meilleure idée des différentes options, voici un aperçu de la façon dont ces notes peuvent être construites dans les différents systèmes d'accord en utilisant des rapports de fréquence entiers, toujours en commençant par C, et comment les résultats se comparent à 12-edo.

http://nbviewer.jupyter.org/gist/leftaroundabout/b0708139f867a160579f14c0b04caeb8

Pythagore, vers le haut

Construit uniquement à partir des quintes et des quarts purs vers le bas (ou de manière équivalente, seulement les quintes vers le haut avec compensation d'octave).

  onKeyboard $ constructNote PreferSharps [3/2, 3/4, 3/2, 3/4, 3/2, 3 / 4, 3/4]  

Pythagore, vers le bas

Cinquièmes vers le bas et quarts vers le haut .

  onKeyboard $ constructNote PreferFlats [4/3, 4/3, 2/3, 4/3, 2/3]  

Donc vous voyez, ce D ♭ est 24ct plus plat que le C♯ de Pythagore.

Ptolémaïque, vers le haut

Construit à partir de quintes et seulement les tiers majeurs vers le haut / les quarts vers le bas.

  onKeyboard $ cons tructNote PreferSharps [3/2, 3/4, 5/4, 3/4]  

Notez que ceci est plus plat que la hauteur de 12 edo. En fait, il est beaucoup plus proche du Pythagorean D ♭ que du Pythagorean C♯!

Il existe une construction alternative qui sort pourtant beaucoup plus plate:

  onKeyboard $ constructNote PreferSharps [4/3, 5/4, 5/8]  

C'est assez extrême, je doute qu'un musicien classique joue jamais du do aussi bas. Mais ici, comme l'a souligné M. Lister dans les commentaires, nous semblons avoir trouvé le 41ct de la réponse de Dorien, à savoir si nous comparons ce C♯ à l'option suivante pour D ♭:

Ptolémaïque, vers le bas

Ici, on atteint D ♭ très rapidement, après seulement un quatrième haut et un tiers majeur vers le bas:

  onKeyboard $ constructNote PreferFlats [4/3, 4/5]  

Alors que diable , vous pouvez bien demander à ceci point. Quelle est la version correcte maintenant?

Eh bien, cela dépend du contexte! Mais bien que cela soit souvent revendiqué - pour la musique classique occidentale, l'accord de Pythagore n'est pas très pertinent. Cette musique fait un usage intensif des harmonies basées sur les accords majeurs , et les accords majeurs ne sont sensés que dans l'accord ptolémaïque , à savoir sous forme de rapports 4: 5: 6, par rapport aux 64 de Pythagore: 81:96. (Personne ne peut réellement distinguer les rapports de fréquence avec des nombres aussi élevés à l'oreille!)

Ainsi, vous pouvez en règle générale dire que C♯ est un peu plus plat que D ♭ . La littérature le confirme, par ex. Leopold Mozart:

... alle durch das (♭) erniedrigten Töne um ein Komma höher als die durch das (♯) erhöhten Noten. Z.B. Des ist höher als Cis; Aussi höher que Gis, Ges höher als Fis usw

Traduction:

Tous les tons abaissés avec (♭) sont une virgule plus haut que le (♯ ) - notes surélevées. Par exemple. D ♭ est supérieur à C♯; A ♭ supérieur à G♯, G ♭ supérieur à F♯ etc.

Il ajoute également

Hier muss das gute Gehör Richter sein

Ici, la bonne audition doit juger

En d'autres termes: il n'y a pas de règle unique que l'on puisse appliquer pour déduire la fréquence parfaite pour une tonalité donnée, il faut toujours écouter soigneusement ce qui sonne le mieux.

La première chose à comprendre est que si vous voulez remonter d'un intervalle constant, vous multipliez la fréquence par un nombre particulier.

Par exemple, pour monter d'une octave, vous multipliez la fréquence par 2. Puisque la multiplication par 2 est la multiplication la plus simple que nous puissions faire, cela semble agréable à l'oreille humaine - si agréable, en fait, que nous apprenons à entendre les deux notes de la même manière.

Si nous voulons monter de deux octaves, nous multiplions à nouveau par 2, pour un total combiné de 4 fois la fréquence d'origine. Et ainsi de suite.

Mais il y a d'autres bons nombres par lesquels nous pouvons multiplier la fréquence. Si on multiplie par 3, par exemple, alors on monte d'une octave et d'une cinquième. Pour obtenir une cinquième, on redescend d'octave en divisant par 2, donc une cinquième correspond à une multiplication par un facteur 3/2 .

Si nous multiplions par 5, alors nous montons de deux octaves et d'une tierce majeure. Un tiers correspond donc à multiplier la fréquence par un facteur 5/4 .

Les tiers, les quintes et les octaves sont fondamentaux pour la musique occidentale, et tous les autres intervalles sont construits à partir d'eux. La raison pour laquelle ils semblent si beaux et concordants est qu'ils sont construits à partir de multiplications très simples.

Par exemple, si nous commençons par C et multiplions par 5/4 , nous arrivons à E , et si nous multiplions encore par 5/4 nous remontons un autre tiers à G♯ . Maintenant, si nous divisons par 3/2 pour descendre d'un cinquième, nous arrivons à C♯ . Le multiplicateur total est

5/4 * 5/4 * 2/3 = 25/24 = 1.041666 ...

Si au contraire on multiplie par 2 , on monte à un C élevé. Maintenant, si nous divisons par 3/2 , nous descendons d'un cinquième à F . Si nous divisons maintenant par 5/4 , nous descendons d'un tiers à D ♭ . Le multiplicateur total est

2 * 2/3 * 4/5 = 16/15 = 1.06666 ...

Puisque ces deux nombres sont si similaires, il est facile de se confondre entre les notes C♯ et D ♭ .

"Maintenant, attendez!" Je vous entends dire. « C♯ et D ♭ ne sont pas simplement des notes similaires - ce sont la même note ! Après tout, ils occupent tous les deux la même touche sur mon clavier de piano! »

C'est en fait un truc musical très intelligent. Pour que les claviers de piano aient un sens, ils ne peuvent pas traiter C♯ et D ♭ comme des notes séparées, du moins pas s'ils veulent éviter quelque chose d'horrible comme celui-ci:

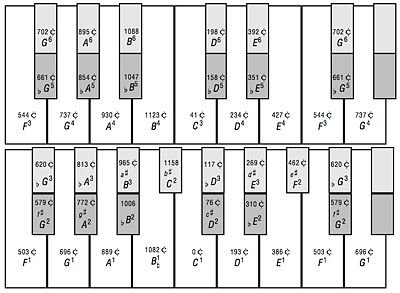
c'est ce qu'on appelle un clavier à touches partagées, du type utilisé au 16ème siècle quand ils figuraient encore ce truc

Au lieu de cela, nous devons approximer les notes afin de pouvoir créer une gamme en utilisant seulement douze tons différents. Nous finissons donc par avoir une clé pour C♯ et D ♭ . Appuyer sur cette touche peut jouer un C♯ , il peut jouer un D ♭ ou il peut jouer quelque chose entre les deux.

Un choix d'approximations s'appelle un tempérament , et de nombreux tempéraments différents ont été utilisés jusqu'à la période classique. Le titre du «Clavier bien tempéré» de J. S. Bach fait référence à un tel tempérament.

Différents musiciens avaient des tempéraments préférés différents. Une qualité commune était que certaines touches (normalement les touches de «note blanche», comme le do majeur) sonneraient très pures et concordantes, tandis que d'autres semblaient plus décalées et épicées. Cela était parfois considéré comme une caractéristique souhaitable d'un tempérament: différentes touches avaient des caractères différents.

Le tempérament utilisé presque universellement sur les pianos modernes est beaucoup plus ennuyeux, mais aussi plus polyvalent. Il s'appelle «Tempérament égal» et son nom signifie que tous les demi-tons du clavier sont exactement au même intervalle. Un demi-ton de tempérament égal est exactement un 12e d'octave, il correspond donc à multiplier la fréquence par

la douzième racine de 2 = 1.05946309436 ....

(remarquez comment cela se situe entre 1.041666 et 1.0666 que nous avons calculé plus tôt!)

Maintenant, à quoi ressemble une cinquième à tempérament égal? Eh bien, cela ressemble à la douzième racine de 2 élevée à la septième puissance (car il y a sept demi-tons dans une quinte parfaite):

2 ^ (7/12) = 1.49830707688 ...

Par une brillante coïncidence mathématique, c'est presque exactement égal à 3/2 . Il n'y a donc pas de différence audible entre une cinquième sur un piano ( 1.498 ... ) et une cinquième que vous chanteriez naturellement ( 1.5 ).

Et le tiers majeur? Une tierce majeure fait quatre demi-tons, ce qui correspond à

2 ^ (4/12) = 1.2599 ...

C'est encore assez proche de 5/4 = 1.25 , mais maintenant la différence est audible (il y a des enregistrements sonores sur https://en.wikipedia.org/wiki/Major_third que vous pouvez écouter ). Une tierce majeure sur un piano est sensiblement différente d'une tierce majeure que vous chanteriez naturellement.

Pour la plupart, vous n'avez pas à vous en soucier trop lorsque vous faites de la musique, mais cela vaut la peine de le garder à l'esprit parfois.

Il y a un accordage pur, où les intervalles sont dans des rapports de fréquence simples, suivant la série harmonique. Cela donne de très beaux accords, mais en une seule tonalité. Changer de clé, vous devez recalibrer. Et les CHANGEMENTS soudains de clé, que la musique d'aujourd'hui fait beaucoup, peuvent sembler un peu bizarres. Il y a donc un système de compromis, un tempérament égal, où tous les demi-tons sont égaux. Ce n'est jamais tout à fait vrai, mais ce n'est pas TROP mal, et nos oreilles s'y sont habituées. C'est ce qu'utilise un piano. Il faut vraiment!

La phrase clé de cette réponse que vous avez manquée était "En réglage de Pythagore…". Comme le dit l'article de Wikipedia,

Le soi-disant "accord de Pythagore" a été utilisé par les musiciens jusqu'au début du 16ème siècle. "Le système de Pythagore semble être idéal en raison de la pureté des quintes, mais d'autres intervalles, en particulier la tierce majeure, sont si désaccordés que les accords majeurs [peuvent être considérés] comme une dissonance."

En raison de l'intervalle de loup, cet accord est rarement utilisé aujourd'hui, bien qu'il soit considéré comme très répandu.

Fondamentalement, la différence entre C♯ et D ♭ est principalement d'ordre historique et théorique intérêt aujourd'hui. C'est précisément à cause de divergences gênantes comme cette différence de 41 cents entre les harmoniques que presque toute la musique moderne préfère d'autres systèmes d'accord.

John Gowers, dans sa réponse, a expliqué comment les intervalles C-C♯ et C-D ♭ peuvent avoir des rapports de fréquence 25:24 et 16:15. 25:24 équivaut à environ 70,67 cents et 16:15 à ~ 111,73 cents. La différence est de 41,06 cents, confirmant ainsi le texte cité par l'OP.

Nous ne devrions pas supposer l'accord de Pythagore, c'est-à-dire construire tous les intervalles à partir d'octaves et de quintes parfaites pures (rapport de fréquence 3: 2). L'accordage pythagoricien est une possibilité mais ce n'est pas la seule disponible.

Encore moins devrions-nous supposer 12ET dans lequel les seuls intervalles possibles sont des multiples d'un demi-ton de 100 centièmes.

une considération générale:

• chaque fréquence enharmonique a une fréquence différente l'une de l'autre;

les gens ignorent simplement que la plupart des cas, soit:

• en raison de l'impossibilité de créer des hauteurs différentes, par exemple sur un violon ou sur à la flûte ou à la trompette, ou à la guitare électrique, le chant n'importe quoi

simplement parce que c'est physiquement extrêmement difficile à faire. ou:

• car dans un instrument comme un piano, par exemple, les hauteurs convergent généralement vers la même tonalité.

mais théoriquement, chaque hauteur enharmonique devrait avoir sa seule intonation, qui selon la note, devrait être:

• 5-10 centimes de distance maximum entre eux;

Cela dépend du réglage. Dans 31-TET, il y a 5 étapes de taille 5 et 2 étapes de taille 3 dans l'échelle de do majeur. Un tranchant ou un plat élève une note de la taille 2 . Par conséquent, C♯ est une 31e octave en dessous de D ♭, ce qui donne 1200cent / 31 = 38,7cent de différence. Eh bien, presque là.

La déclaration originale parle probablement d'une forme d'accord pythagoricien ou pur, mais on ne sait pas exactement quelle échelle et quel réglage sont utilisés pour la déclaration.